In this article the use of a Mil-Dot or similar reticle in riflescope for distance assessing, long range bullet drop compensation and wind compensation will be introduced. The article is written in a very simple language and therefore all explanations, terms and concepts are simplified as much as possible.
The reticle
The use of a reticle in order to asses distance and to compensate bullet trajectory firstly requires the right kind of reticle which has to be placed in the first focal plane or the riflescope has to be set to specific magnification at which the reticle subtentions are accurate in miliradians. The appropriate reticles are those that have additional measuring points in all directions along with the central targeting point. The easiest way is to use reticles that have these spacing lines in miliradians (mrad) and this concept is the main material for this article. There are also differently marked reticles that have markings in minutes of angle (MOA), but that will be the subject of another article.
We have already mentioned that the best option is to have a reticle that is set in the first focal plane of a riflescope. It is because this way the reticle always remains in the same proportion to the object. For example, take a reticle that has two markings which would represent 10 cm on a distance of 100 meters. When the reticle is set in the first focal plane it will thicken or thin when magnifying but the dots will always remain 10 cm apart at a distance of 100 meters. If the reticle is set in the second focal plane it will not change but will remain the same size no matter the magnification. But only at one specific magnification will the two markings be 10 cm apart at a distance of 100 meters and different at any other magnification.
There are a couple of new and cheap products on the market that offer bullet drop compensation reticles set in the second focal plane (common SFP BDC scopes in sub 1000€ price range), but this is only a marketing stunt to attract buyers, because the marked dots are really accurate only at maximum or at some other predefined magnification. The second big problem with this type of scopes is that bullet trajectories vary considerably in regard to different calibers, barrel lengths, bullet weights and so on. It would be nice if the solution to a problem as complicated as bullet drop compensation would be so simple as cheap BDC scopes are implying but unfortunately it is not.
Luckily more and more manufacturers started to produce riflescopes with reticles set in the first focal plane that are much cheaper and more affordable (products such as Kaps Tactical, Vortex, IOR, Sightron, Athlon) and there is more and more people who understand how to use them. Such riflescopes are called MIL/MIL scopes.
Picture 1 shows us the most frequently used reticles with miliradian markings. By far the most widespread one is the Mil-Dot that has 1 miliradian markings in all directions. Other reticles have markings that represent 0,5 or even 0,2 miliradians and are more Brand specific.

Miliradians
Before we continue with reticle use it would be a good idea to refresh geometry basics and explain what radians and miliradians actually are. In everyday life the use of degrees is much frequently used as opposed to radians but when it comes to shooting the story is quite the opposite and almost no one uses degrees anymore. The definition of a radian on Wikipedia is:
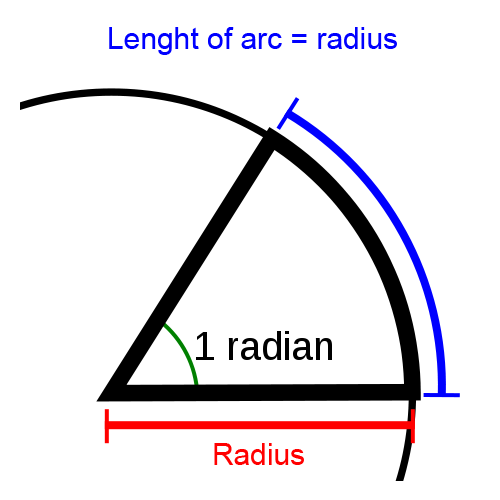
“The radian is the standard unit of angular measurement. Radian is the ratio between the length of an arc and its radius. “
A better way to explain what a radian is to explain it with the following picture. An angle of 1 radian results in an arc with a length equal to the radius of the circle.
For an even easier explanation the following picture where radians and degrees are compared might also help. A circle has 360 degrees or 2π radians. Therefore a circle has 2 X 3,14159 radians or 6,28318 radians. Every radian consists of a 1000 miliradians and therefore there are 6283,18 miliradians in a circle. We can also say that a circle can be divided into 360 X 60 = 21600 degree minutes. Picture 3 shows us two different markings of radians and one marking for degrees. The outer and longer markings represent radians and the smaller inner markings represent miliradians. The longer inner markings represent degrees.

It is now clearer what a radian is but why reticles are marked in miliradians is perhaps still not as much. This is simply because miliradians can be very easily converted to a decimal system of distance measurement. In an angle of 1 miliradian and a diameter of 100 meters, the distance of arc length will be 0,1 meters or 10 cm. For simplification we can say that arc curvature at this distances is almost flat and we will not make a big mistake with this assumption. With a diameter of 200 meters it will be 0,2 meters or 20cm, with a diameter of 500 meters it will be 0,5 meters-50cm and with a diameter of 1000 meters it will be 1 meter. If the reticle of a riflescope has two markings at a distance of 1 miliradian and we are targeting at a distance of 100 meters this will mean that two dots on a target are 0,1 / 10 cm apart. The same goes for any figure as shown in table 1, where the spacing between two dots on a target is 1 miliradian.

The use of miliradians for bullet drop compensation and wind compensation
When we use a riflescope with miliradian markings in combination with laser distance measurement (or we asses the distance with the reticle it self) it is possible to compensate bullet trajectory without having to adjust the reticle’s position using clicks on the turrets. Let’s say we are using a .308 winchester caliber rifle and a RWS KS 10.7 g (165gr) bullet which has ballistic specifications listed in table 2.
The reticle in picture 5 shows us different points to target at different distances in order to compensate for bullet drop during flight. In a reticle that is set in the first focal plane the dots will be located in the proper spot no matter the magnification.

The same principle can be used for wind compensation but the wind speed, distance and other bullet specifications must be known. We will not go into such detail in this article.
The use of miliradians for distance assessment
Since it is possible to compensate bullet drop and wind compensation with reticles in miliradians they can be also used for distance assessment of objects. The later is very complicated and needs a lot of practice. The most important thing is to know the size of the object we are looking at. The mathematical derivation of distance assessment is pretty easy and we will not spend any more time on this issue. But if anyone would like to know the derivation process just contact us and the whole mathematical process will be supplied.
If the dimensions of an object are known it is possible to calculate the distance using the reticle. In picture 6 a Mil-Dot reticle with 1 miliradian marking is shown. The car with its height of 1.4 meters represents 2 miliradians and this allows us to calculate the distance.
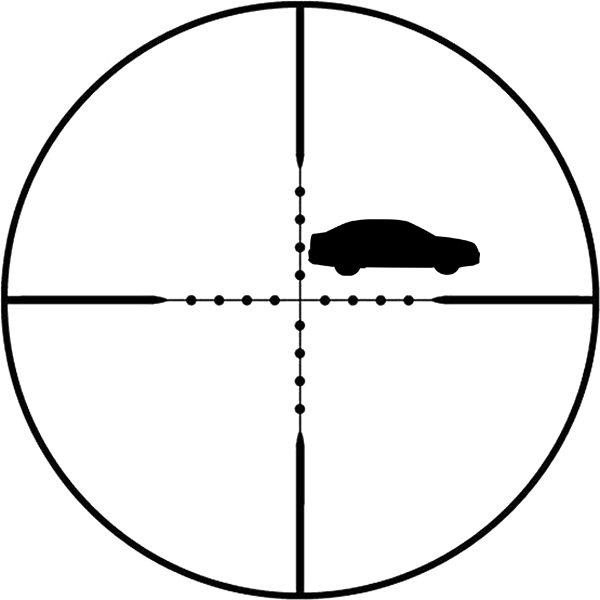
The distance is calculated using the following equation:

D is distance, h is the dimension of the object and x is the miliradian value on the reticle.





true